Vol. 16 No. 2 (2025): (Regular Issue in Progress)
Research Article

Statistical Reliability of the Modified Areal Weighted by Control Zones Method to Spatially Downscale Individual Social Data

PDF
Najla Touati
LISST, UMR 5193, Toulouse Jean Jaures University, 5 allée A. Machado, Toulouse, 31058, France
Wilda Jean Baptiste
LISST, UMR 5193, CNRS, 5 allée A. Machado, Toulouse, 31058, France
Julia Hidalgo
LISST, UMR 5193, CNRS, 5 allée A. Machado, Toulouse, 31058, France
Description of the data processing performed in this study to evaluate the downscaling of social data from a coarse mesh to a finer mesh
DOI: https://doi.org/10.48088/ejg.n.tou.16.2.268.285
Categories

Published 2025-07-24

Keywords

  • Downscaling social data,
  • upscaling social data,
  • aggregation,
  • disaggregation,
  • mesh,
  • spatial analysis,
  • topographical reference unit (RSU)
    • ...More
    Less

How to Cite

Touati, Najla, Wilda Jean Baptiste, and Julia Hidalgo. 2025. “Statistical Reliability of the Modified Areal Weighted by Control Zones Method to Spatially Downscale Individual Social Data”. European Journal of Geography 16 (2):268-85. https://doi.org/10.48088/ejg.n.tou.16.2.268.285.

Copyright (c) 2025 Najla Touati, Wilda Jean Baptiste, Julia Hidalgo

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Received 2025-02-21
Accepted 2025-07-19
Published 2025-07-24

Abstract

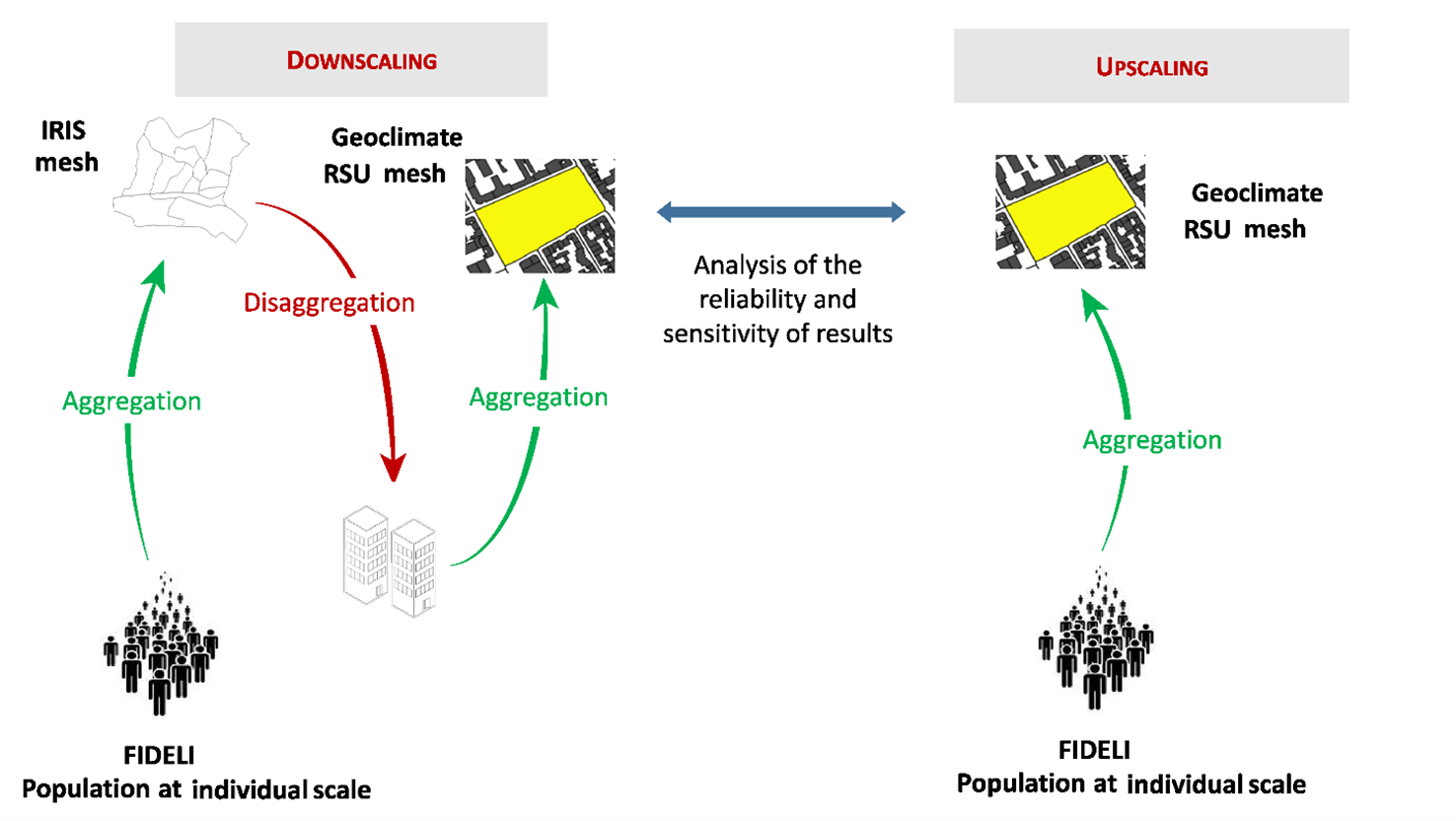
This study evaluates the modified areal weighting by control zones method (MAW-CZ) often involved in downscaling social data from a large spatial mesh, to a smaller mesh. This method has been extensively used in literature but the impossibility, until recently, of accessing individual data makes it so that it has not been evaluated.  In this study it is applied to two case studies, Toulouse and Grenoble-Alpes Metropoles, using the census INSEE data at the IRIS scale and the building islet or topographical reference units (RSU) scale. The study found that 27.2% of RSUs in the Toulouse metropolis and 21.9% in the Grenoble-Alpes metropolis are inhabited, with mean populations of 122 and 116 residents, and maximum populations of 2,429 and 6,451 residents, respectively in 2018. The chosen downscaling approach introduces small errors for small and medium-sizedRSUs. For example, 94%, 78%, and 72% of RSUs of <100, 101–255, and 256–500 inhabitants, respectively, are correctly classified by the modified areal weighting by control zones method in the Toulouse Metropole. However, there are significant differences for the most populated RSUs (the performance decreases to 60% for RSUs with more than 500 inhabitants), with this category having a representativeness of 8.4% and 7.2% of the total number of inhabited RSUs in the Toulouse and Grenoble-Alpes metropoles, respectively. The spatial distribution of the biased RSUs are nevertheless homogeneous throughout the two territories. These discrepancies are due to both the upscaling/downscaling methods used and the nature of the data (points in the upscaling and polygons in the downscaling).

Highlights:

  • Population is downscaled from the census IRIS scale, to the RSU scale.
  • Modified areal weighted by control zones approach is evaluated.
  • Downscaling performs for small and medium-sized RSUs, <500 inhabitants with errors between 2 and 28%.
  • RSUs with >500 inhabitants — where errors reach 40% — represent <10% of inhabited RSUs in both case studies.
PDF

Downloads

Download data is not yet available.
Crossref
Scopus
Google Scholar
Europe PMC

References

  1. Anselin, L. (1995). Local Indicators of Spatial Association — LISA. Geographical Analysis, 27(2), 93–115. https://doi.org/10.1111/j.1538-4632.1995.tb00338.x
  2. Arbia, G. & others. (1989). Statistical effect of spatial data transformations: A proposed general framework. In Accuracy of spatial databases (p. 249 249). Taylor and Francis New York.
  3. Batsaris, M., Zafeirelli, S., Vaitis, M., & Kavroudakis, D. (2023). PoD: A Web Tool for Population Downscaling Using Areal Interpolation and Volun-teered Geographic Information. European Journal of Geography, 14(4), 22–36. https://doi.org/10.48088/ejg.m.bat.14.4.022.036
  4. Bocher, E., Petit, G., Bernard, J., & Palominos, S. (2018). A geoprocessing framework to compute urban indicators: The MApUCE tools chain. Urban Climate, 24, 153 174. https://doi.org/10.1016/j.uclim.2018.01.008
  5. Bocher, E., Bernard, J., Wiederhold, E. L. S., Leconte, F., Petit, G., Palominos, S., & Noûs, C. (2021). GeoClimate: A Geospatial processing toolbox for environmental and climate studies. Journal of Open Source Software, 6(65), 3541. https://doi.org/10.21105/joss.03541
  6. Do, V. H., Thomas-Agnan, C., & Vanhems, A. (2015). Spatial reallocation of areal data – another look at basic methods. Revue d’Économie Régio-nale & Urbaine, 1, 27 58. https://doi.org/10.3917/reru.151.0027
  7. Fotheringham, A. S., & Wong, D. W. S. (1991). The Modifiable Areal Unit Problem in Multivariate Statistical Analysis. Environment and Planning A: Economy and Space, 23(7), 1025-1044. https://doi.org/10.1068/a231025
  8. Fotheringham, A. S., & Sachdeva, M. (2022). Scale and local modeling: New perspectives on the modifiable areal unit problem and Simpson’s paradox. Journal of Geographical Systems, 24(3), 475 499.
  9. Flowerdew, R., & Green, M. (1992). Developments in areal interpolation methods and GIS. The Annals of Regional Science, 26(1), 67 78. https://doi.org/10.1007/BF01581481
  10. Goodchild, M., Anselin, L., & Deichmann, U. (1993). A Framework for the Areal Interpolation of Socioeconomic Data. Environment and Planning A, 25, 383 397. https://doi.org/10.1068/a250383
  11. Hidalgo, J., Touati, N., Haouès-Jouve, S., Jégou, L., Bretagne, G., Bocher, E., Masson, V., Mayis, A., Jougla, R., Petit, G., & Schoetter, R. (2023). Mapping the urban climate to address summer comfort management in French urban planning documents. Cybergeo : Revue européenne de géographie / European journal of geography. https://doi.org/10.4000/cybergeo.40319
  12. Insee & Ministère des Finances (DGFiP) [Producteur], Fichier DÉmographique sur les Logements et les Individus - 2018 [Fichiers de données], Centre d'Accès Sécurisé aux Données (CASD) [Diffuseur], http://doi.org/10.34724/CASD.295.3257.V1
  13. King, G., Rosen, O., & Tanner, M. A. (Éds.). (2004). Ecological inference: New methodological strategies. Cambridge University Press.
  14. Langford, M., & Unwin, D. (1994). Generating and Mapping Population Density Surfaces within a GIS. The Cartographic Journal, 31, 21 26. https://doi.org/10.1179/000870494787073718
  15. Louvet, R., Josselin, D., Genre-Grandpierre, C., & Aryal, J. (2015). Impact du changement d’échelle sur l’étude des causes des feux de forêts du sud-est de la France. SAGEO1. https://ceur-ws.org/Vol-1535/paper-18.pdf
  16. Masson, V., Hidalgo, J., Amossé, A., Belaid, F., Bocher, E., Bonhomme, M., Bourgeois, A., Bretagne, G., Caillerez, S., Cordeau, E., Demazeux, C., Faraut, S., Gallato, C., Haouès-Jouve, S., Lambert, M.-L., Lemonsu, A., Lestringant, R., Levy, J.-P., Long, N., … Vye, D. D. (2015, juillet). Urban Climate, Human behavior & Energy consumption: From LCZ mapping to simulation and urban planning (the MapUCE project). 9th Interna-tional Conference on Urban Climate. https://hal.science/hal-01252761
  17. Monteiro, J., Martins, B., & Pires, J. M. (2018). A hybrid approach for the spatial disaggregation of socio-economic indicators. International Jour-nal of Data Science and Analytics, 5(2), 189 211. https://doi.org/10.1007/s41060-017-0080-z
  18. Moran, P. (1950) A Test for the Serial Independence of Residuals. Biometrika, 37, 178-181. http://dx.doi.org/10.1093/biomet/37.1-2.178
  19. Nordhaus, W. D. (2002). Alternative Approaches to Spatial Rescaling. (Yale University, New Haven, CT) https://gecon.yale.edu/sites/default/files/files/gecon_data_20051206_3.pdf
  20. Openshaw, S., Taylor P.J. (1979). A million or so correlation coefficients: three experiments on the modifiable areal unit problem, Statistical applications in the spatial sciences, 1979, vol. 21, p. 127 -144.
  21. Openshaw, S. (1981). Le problème de l’agrégation spatiale en géographie. L’Espace géographique, 10(1), 15 24. https://doi.org/10.3406/spgeo.1981.3599
  22. Pivano, C., Bonin, O., & Hubert, J.-P. (2015). Transfert de support de données de déplacements : Quelles données de contrôle, et jusqu’à quelles échelles? Journées de méthodologie statistiques, 26p. https://hal.science/hal-01217297
  23. Plumejeaud, C., Prud’homme, J., Davoine, P.-A., & Gensel, J. (2010). Transferring Indicators into Different Partitions of Geographic Space. In D. Taniar, O. Gervasi, B. Murgante, E. Pardede, & B. O. Apduhan (Éds.), Computational Science and Its Applications – ICCSA 2010 (Vol. 6016, p. 445 460). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-12156-2_34
  24. Robinson, W. S. (1950). Ecological Correlations and the Behavior of Individuals. American Sociological Review, 15(3), 351 357. https://doi.org/10.2307/2087176
  25. Rome, S., Bigot, S., Foissard, X., Madelin, M., Duche, S., & Fouvet, A.-C. (2020). Les deux épisodes caniculaires de l’été 2019 à Grenoble : Constat et perspective pour une gestion des extrêmes thermiques futurs. Climatologie, 17. https://doi.org/10.1051/climat/202017012
  26. Simpson, E. H. (1951). The Interpretation of Interaction in Contingency Tables. Journal of the Royal Statistical Society. Series B (Methodological), 13(2), 238 241.
  27. Vignes, C., & Rimbourg, S. (2013). Méthodes statistiques d’allocation spatiale : Interpolation de données surfaciques. 79.
  28. Wong, D. W. S. (2004). The Modifiable Areal Unit Problem (MAUP). In D. G. Janelle, B. Warf, & K. Hansen (Éds.), WorldMinds: Geographical Per-spectives on 100 Problems: Commemorating the 100th Anniversary of the Association of American Geographers 1904–2004 (p. 571 575). Springer Netherlands. https://doi.org/10.1007/978-1-4020-2352-1_93